Mrówka: Dana jest łamana zwyczajna zamknięta ABCD taka że |AB| >0, |BC|=|AB|+1, |AD|=|CD|+1, |CD|=|BC|+1. Uzasadnij że figura wyznaczona przez te łamaną nie może być trapezem.

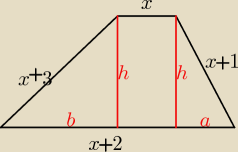
Basia: przypuśćmy, że to jest trapez wtedy a+b = x+2 − x = 2 b = 2−a h² = (x+1)² − a² h² = (x+3)² − b² −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 0 = (x+3)³ − b² − (x+1)² + a² x²+6x+9 − x² − 2x − 1 = b² − a² 4x + 8 = (2−a)² − a² 4(x+2) = 4 − 4a + a² − a² 4(x+2) = 4(1−a) x+2 = 1−a a = 1−2−x = −x−1 < 0 a to jest niemożliwe

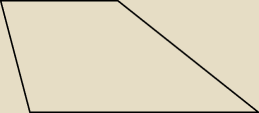
Basia: P.S. trzeba jeszcze rozpatrzyć drugi przypadek; to też jest trapez